n alternative to Macaulay's duration is Fisher-Weil duration, which takes advantage of the forward markets to trade interest rate risk directly. Macaulay's duration measures the change in the price of a bond due to a change in the bond's internal rate of return. A fixed-income security’s yield to maturity can be derived once the market value of the security is known. The market value, in turn, is determined from the yield curve. Therefore, a potentially more useful measure is one that examines shifts in the yield curve at the primitive level of forward interest rates.

Recall that the spot rate is defined as the geometric average of the current spot and forward rates, and thus a change in any forward rate can impact upon a wide range of spot rates. A measure of duration that is linked to forward/spot rate changes can be defined as follows.

Let 1 + ₀r_T denote the spot yield to maturity of a t-period discount bond. Then, the current price of cash flows C1,..., CT is given by

A parallel shift in the yield curve then consists of perturbing every yield by a constant amount, say d.

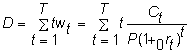
Finally, we can define a measure of duration directly in terms of perturbations in the forward rates. Let ft denote the forward rate between periods t - 1 and t. Then,

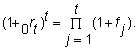
If we perturb all forward rates by d , we get

and

This leads to the following measure of duration:

The bond immunization theorem also holds for this definition. In fact, it is not necessary that there be a parallel shift in the forward rates. The theorem still holds if ft is perturbed to ft + d (t), as long as d (t) is an increasing function of t.

In the next topic, Hedging Using Futures Contracts, we will construct hedge ratios for futures contracts.