3.6 Arbitrage and Synthetic Coupon Bonds

3.6 Arbitrage and Synthetic Coupon Bonds

n the example developed in Topic 3.4, Pricing Relative to the Yield Curve, a synthetic coupon bond also can be created. This is a portfolio that does not include the true coupon bond but that exactly replicates the timing and magnitude (and default risk) of cash flows that an investor would receive from the coupon bond. The coupon bond can then be priced directly from arbitrage arguments applied to this synthetic security.

You can create a synthetic coupon bond from a portfolio of zero-coupon bonds. The portfolio is constructed so that the cash flows from the face amounts of the portfolio of zero-coupon debt contracts exactly replicate the cash flows from ten coupon bonds.

The replicating portfolio is straightforward to construct. Consider a portfolio that consists of +1 one year zeroes, +1 two year zeroes and 11 three year zeroes. Observe that this portfolio provides the following cash flows:

Synthetic Coupon Bond	Cost	Cash Flow Per Year
+1 One year Zeroes	$96.1538	$ 100
+1 Two year Zeroes	$87.4092	$ 100
+11 Three year Zeroes	$828.9306	$1100
Total	$1012.4900

This portfolio exactly replicates the cash flows provided from a portfolio of ten coupon bonds. The market value of this portfolio of zero-coupon bonds determines the arbitrage-free value of the coupon bond.

Recall in the example provided in Topic 3.4, the spot interest rates are 4%, 6.96%, and 9.89%, for Years 1-3, respectively. Discounting at these rates the value of the synthetic portfolio we have created is $1,012.49. This implies an arbitrage-free value of $101.25 for one coupon bond, which is exactly what we concluded in Topic 3.4.

Now you are ready to solve the value for each bond.

Yields to Maturity and Upward Sloping Yield Curves

The yield to maturity from the coupon bond is computed numerically by solving for the interest rate r that equates the present value of the cash inflows to the bond’s price.

You can verify that if the price of the bond is $101.25, the yield to maturity is 9.502% per year. Before you can actually earn this yield to maturity, however, you must reinvest all cash proceeds (the coupons) prior to maturity at the yield to maturity. If you invest them for less, your actual return will be lower.

In the example provided in Topic 3.4, the spot interest rates are 4%, 6.96%, and 9.89%, for Years 1-3, respectively. Online below, you can change the first three spot rates by double-clicking and typing directly into each yield cell on the RHS of the above screen. You should delete the remaining rows by clicking in the cell with "Period" and right click the mouse to bring up the Delete Row, Insert Row option as displayed

9e.g., the last remaining row to be deleted is row 10 in this example).

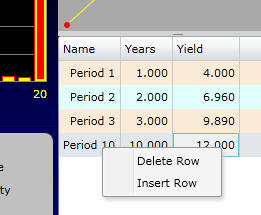
Set up this way you have recreated the simple upward sloping yield curve as plotted. This yield curve is then used to calculate the present value of the bond which you can verify is $101.25. Finally, you can verify that is you had used the constant discount rate of 9.502%. This is a weighted average of the upward sloping yield curve with the majority of the weight being placed on the period 3 spot rate of interest because both the face value and the coupon payment is made at the end of period 3.

You can now verify the above online.

Once you have verified the above example now change the shape of the yield curve to see how this impacts the yield to maturity. Typically, you will not be able to reinvest the intermediate coupons at the yield to maturity because it is a time weighted average which does not coincide with any of the spot rates. This underlies the importance of the yield curve itself. The yield curve tells you the interest rate that is available for the reinvestment of coupon payments.

Figure 3.6: Coupon Reinvestment Rates

In Figure 3.6, you can see that we are really interested in the interest rate that is applicable for the time periods Year 1 to Year 2 and Year 2 to Year 3. These are not the spot interest rates but instead the forward interest rates. These rates are the focus of our discussion in Topic 3.7, Forward Interest Rates.